Can you solve it? Tiler swift – Guardian

Apologies to any Antipodean Swifties arriving on this internet page. On the present time’s puzzle is ready tiles, and whether or no longer you would possibly maybe be in a procedure to solve it impulsively.
The puzzle concerns sunless and white tiles on a 4×4 grid. Accumulate in mind the image under, which highlights adjacent rows in the grid.

For every cell in a top row, there are two picks for the cell straight under it: either it has the a similar color, or it has a particular color.
As an instance, in the checkerboard sample, under left, every tile in the tip row has a tile in a particular color under it. Likewise for row 2 and row 3.
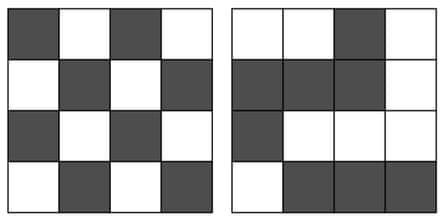
For the grid on the exact, two of the tip row tiles enjoy a particular color straight under them, and two enjoy the a similar color straight under them. For the second row, again, two enjoy a particular color under them, and two the a similar color. The sample breaks down, nonetheless, in the third row, where all four tiles enjoy a particular color under them.
Challenge tile
Your assignment is to search out a approach to tile the grid such that:
1) For every row (other than the underside one), two tiles enjoy the a similar color straight under them and two tiles enjoy a particular color.
2) For every pair of adjacent columns, (proven under) two tiles in the left column enjoy the a similar color straight to the exact and two tiles in the left column enjoy a particular color to the exact.

While you chanced on that straightforward, right here’s one for the professionals: are you able to tile an 8×8 gird the a similar approach? That is, such that for every pair of adjacent rows/columns matches, the tiles match in half the positions and vary in half of the positions?
I’ll be support with a alternatives at 5pm UK.
NO SPOILERS Please discuss your popular tilers, Tylers, Taylors and/or swifts as an different.
On the present time’s puzzle modified into as soon as devised by maths outreach legends Katie Steckles and Peter Rowlett, who along with Sam Hartburn and Alison Kiddle are the authors of Short Cuts: Maths, which supplies bite-sized introductions to many mathematical tips. One topic included is matrices and block designs, an introduction to which is this very puzzle.
Katie and Peter are also both section of Finite Crew: an on-line neighborhood for americans drawn to taking half in with mathematical tips – with monthly livestreams and dialogue, as effectively as a feed of attention-grabbing maths snort material from all over the attach the on-line. Talk about with patreon.com/finitegroup to substantiate in.


